3. Метод итераций

Метод итераций — один из наиболее продуктивных методов поиска корней уравнений для нужд школьной физики. С одной стороны его достаточно просто реализовать, с другой метод универсален (почти).

Рассмотрим произвольное уравнение вида:

\[ F(x) = 0, \]

и попробуем найти его решения. Для этого заменим это выражение на эквивалентное (множество решений не должно измениться) следующего вида:

\[ f(x) = x. \]

Тогда алгоритм, приводящий к решению, выглядит так:

\[ x_{n+1} = f(x_n), \]

однако возникает сложность: чему равен \( x_1 \)? В простом случае первое значение выбирается близко к предполагаемому значению корня.

3.1. Пример 1

Рассмотрим уравнение:

\[ x^3 - 2x + \frac{1}{2} = 0, \]

найдем его корни. Этому уравнению эквивалентно такое:

\[ x = \frac{2}{x} - \frac{1}{2x^2}. \]

Полученный итерационный алгоритм позволяет достаточно быстро получить оценку корня, так значения \( x \) на 7 и 8 итерации составляют примерно 1.37 и 1.19, при этом значение корня составляет около 1.27 (при начальном значении \( x_1 = 2 \)).

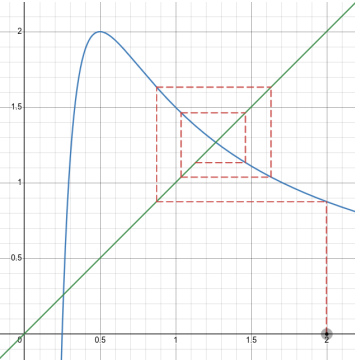
Рис. 1: Метод итераций

На практике удобно вычислять такие итерационные схемы с помощью калькулятора с переменной \( Ans \):

\[ Ans_2 = \frac{2}{Ans_1} - \frac{1}{2Ans_1^2}. \]

В ходе решения задачи можно столкнуться с затруднением: метод итераций не всегда сходится. Рассмотрим такое уравнение:

\[ x^6 - 5x - 2 = 0. \]

Возможны следующие реализации итерационного алгоритма:

\[ x_{n+1} = \frac{x_n^6 - 2}{5}, \]

\[ x_{n+1} = \frac{5}{x_n^4} + \frac{2}{x_n^5}, \]

\[ x_{n+1} = \sqrt[6]{5x_n + 2}, \]

\[ x_{n+1} = \sqrt{\frac{5}{x_n^3} + \frac{2}{x_n^4}}. \]

Первый алгоритм сможет дать лишь один из двух корней, только если \( x_1 \in [-1, 1] \) (в остальных случаях алгоритм не сойдется). Второй и четвертый разойдутся всегда. Лишь третий покажет хорошую сходимость при почти любом начальном значении (но снова доступен лишь один из двух корней). В этом контексте возникает необходимость в критерии сходимости для итерационного метода. Он формулируется так: итерационный алгоритм сходится для множества значений \( x \), если:

\[ |f'(x)| < 1. \]

3.2. Пример 2

Найдем ширину функции \( y = xe^{-x} \) на полувысоте.

Сначала найдем максимальное значение функции:

\[ y' = e^{-x} - xe^{-x} = 0. \]

Это справедливо для \( x = 1 \). То есть максимальное значение функции \( y_{max} = \frac{1}{e} \).

Чтобы найти ширину функции на полувысоте, надо найти решения уравнения (ожидаем, что решения два):

\[ y = xe^{-x} = \frac{1}{2e}. \]

Рассмотрим итерационный алгоритм:

\[ x_{n+1} = f(x) = \frac{e^x}{2e}. \]

Проверим критерий сходимости:

\[ f'(x) = \frac{e^x}{2e}, \]

\( |f'(x)| < 1 \) при \( x < 1 + \ln(2) \approx 1.7 \). Эта граница правее максимума функции, а значит этот алгоритм позволит найти левый корень уравнения (эту границу нужно учесть при подборе первого \( x \) !!!)

Для правого придется подобрать другой алгоритм, например, такой:

\[ x_{n+1} = \ln(2ex_n); \]

\[ f'(x) = \frac{1}{x}, \]

\( |f'(x)| < 1 \) при \( x > 1 \). Этот алгоритм пригоден для поиска правого корня уравнения.

Методом итераций получаем два корня: 0.23 и 2.68 (примерно), ширина исходной функции - разность двух корней, она составляет 2.45.

Рис. 2: График функции \( y = xe^{-x} \) , горизонтальной прямой отмечена полувысота.