4. О брахистохроне

4.1. Краткое введение

В тексте рассматриваются два решения проблемы поиска брахистохроны, предложенные математиком Марком Леви. Сам автор опубликовал одно из них в небольшой заметке, представляя его как краткое и уникальное (публикация достаточно свежая), но там оно не вполне подробно описано. Однако Леви ссылается на свою книгу “Classical Mechanics with Calculus of Variations and Optimal Control”, в которой изложены различные вопросы, смежные для механики и математического анализа. Благодаря последовательному изложению теории, сложный вариант решения задачи может стать доступным даже читателю с минимальной подготовкой. В этом материале изложены необходимые определения и теоремы, предложенные автором, а также рассматривается простое решение задачи без погружения в математику.

4.2. Лагранжиан

Положим, что материальная точка движется по оси \( x \) под действием некоторой силы \( F(x) \).

Тогда запишем для нее разность кинетической и потенциальной энергии:

\[ L(x, \dot{x}) = \frac{m\dot{x}^2}{2} - U(x). \]

Будем считать, что \( x \) и \( \dot{x} \) — независимые друг от друга функции, параметризованные временем \( t \). Обозначим частные производные \( L \) так:

\[ \frac{\partial L}{\partial x} = L_x = -U'(x), \quad \frac{\partial L}{\partial \dot{x}} = L_{\dot{x}} = m\dot{x}. \]

В таких терминах выражение \( m\ddot{x} = -U'(x) \) можно записать как \( \frac{d}{dt}L_{\dot{x}} = L_x \), это называют уравнением Эйлера-Лагранжа. Докажем его справедливость, а также ряда других полезных утверждений.

Рассмотрим траекторию на плоскости \( t, x \). Пусть \( x(t_0) = x_0 \), \( x(t_1) = x_1 \) — начальная и конечная точки соответственно (точки \( A_0 \),\( A_1 \), см. рисунок 1). Введем отображение из множества кривых с таким началом и концом на \( R \) действительные числа:

\[ S[x] = \int\limits_{t_0}^{t_1} L(x, \dot{x}) dt. \]

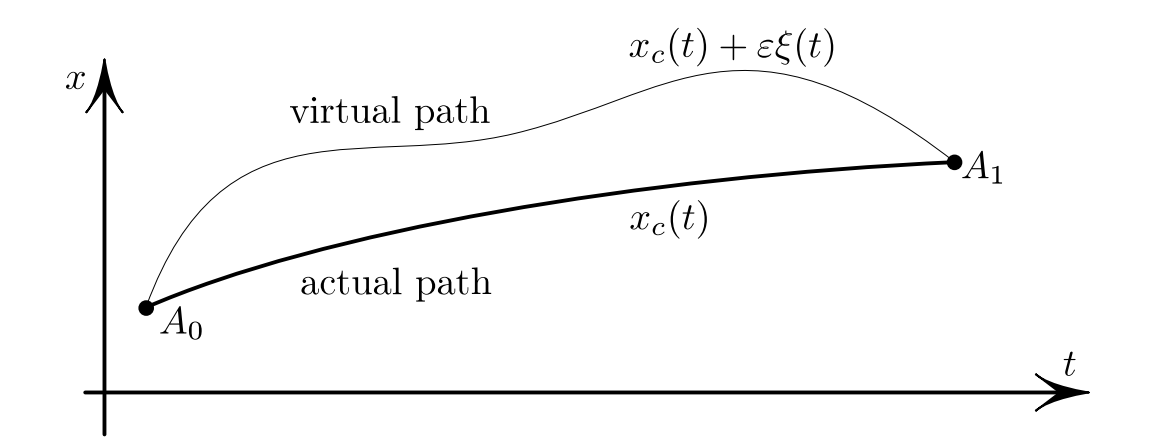
Рис. 1: Множество кривых

Функцию \( x \) называют критической для данного \( S \), если выполняется следующее:

\[ \frac{d}{d\epsilon} S[x_c + \epsilon\xi] = 0|\epsilon = 0, \]

для любой функции \( \xi \), при условии, что \( \xi(t_0) = \xi(t_1) = 0 \).

Принцип Гамильтона гласит: \( x \) тогда и только тогда повторяет траекторию тела, когда \( x \) критическая для конкретного уравнения движения в предложенном виде (одна из формулировок). Это сильное утверждение, доказательство которого выходит за рамки текущего рассуждения. Однако некоторую связь, достаточно важную, из определения критической функции получить можно.

4.2.1. Теорема 1: Уравнение Эйлера-Лагранжа

Положим, что \( L(x, \dot{x}) \) имеет две непрерывные производные в своих переменных. Если \( x = x(t) \) — критическая для данного \( L \), то выполняется равенство:

\[ \frac{d}{dt}L_{\dot{x}} = L_x. \]

В качестве примера использования такого уравнения можно использовать выражение для гармонических колебаний.

Доказательство

Из того, что \(x\) - критическая, следует:

\[ \frac{d}{d\varepsilon}\int\limits_{t_0}^{t_1}L( x+\varepsilon\xi, \dot x+\varepsilon\dot\xi)dt=0|\varepsilon=0, \]

откуда получаем:

\[ \int\limits_{t_0}^{t_1} \left( L_x-\frac{d}{dt}L_{\dot x}\right)\xi dt = 0. \]

Если равенство не выполнено, то левая часть ненулевая для некоторой точки из интервала \((t_0, t_1)\) вместе с какой-то ее окрестностью. Тогда подберем \(\xi\) так, чтобы в этой окрестности содержалась точка с \(\xi(\tilde t)>0\). Значит, существует точка, в которой всё выражение не равно нулю, противоречие. Значит, равенство \( \frac{d}{dt}L_{\dot{x}} = L_x \) выполняется.

4.2.2. Теорема 2: Частный случай теоремы Нётер

Для каждого \( x \) решения уравнения Эйлера-Лагранжа верно следующее:

\[ \dot xL_{\dot x} - L = const. \]

Доказательство

Продифференциируем:

\[ \frac{d}{dt}(\dot xL_{\dot x} - L)=\ddot xL_{\dot x}+\dot x\frac{d}{dt}L_{\dot x}-L_x\dot x - L_{\dot x}\ddot x = 0. \]

Для указанного в начале частного примера эта теорема дает ЗСЭ, в таком виде она будет полезна и далее, хотя получена довольно просто.

4.3. Особый класс Лагранжиан

Далее будем работать с более узкой сущностью:

\[ S = \int\limits_{b}^{a} F(y) \sqrt{1 + y'^2} dx = \int\limits_{b}^{a} F(y) ds. \]

4.3.1. Теорема 3

Если \(y=y(x)\) минимизирует \(S\) из пердыдущего определения на некотором конечном интервале, тогда \(y\) удовлетворяет условию:

\[ \frac{F(y)}{\sqrt{1 + y'^2}} = F(y)\sin\theta = const. \]

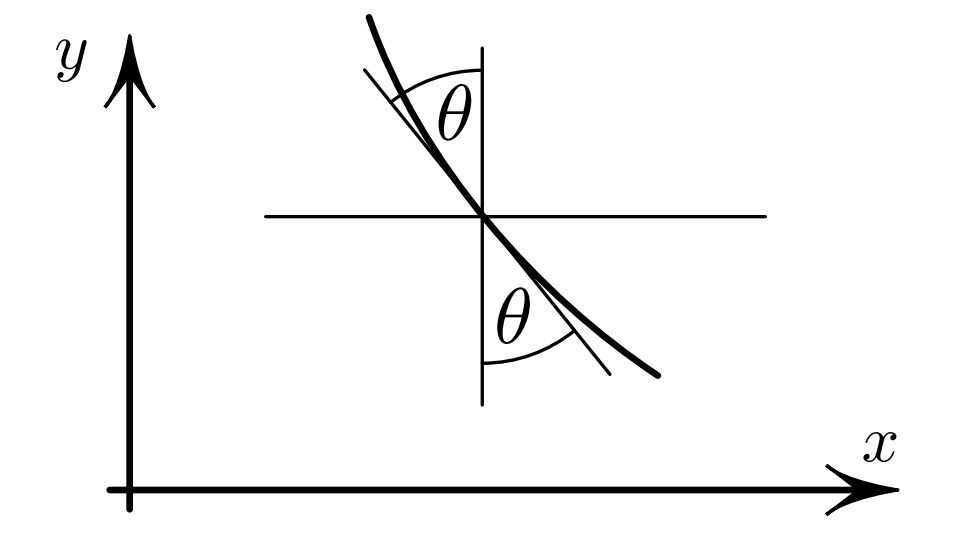
Рис. 2: Определение угла \( \theta \)

Доказательство

Поскольку подинтегральное выражение не зависит от \(x\), можно применить теорему Нётер:

\[ L = F(y)\sqrt{1+y'^2},\; y'L_{y'}-L=const. \]

После упрощения получаем нужный результат.

4.4. Сильно более простой путь

Есть способ получить последний результат, важный для дальнейшей работы, не прибегая к столь сложным конструкциям, показанным выше.

Нам все так же нужно минимизировать интеграл \( S = \int\limits_{b}^{a} F(y) ds \). Представим его как дискретную сумму потенциальных энергий пружин особой конструкции: энергия пропорциональна растяжению, сами пружины расположены на особом стенде с горизонтальными стержнями, края пружин соеденены кольцами, движущимися по стержням без трения. Вертикальный отступ между стержнями одинаков, конечные точки заранее фиксированы:

\[ \sum_{k=1}^n F_k\Delta s_k, \]

где \(\Delta s_k\) - длина натяжения \(k\)-ой пружины на рисунке 3. Поскольку принцип наименьшего действия выполнится и в такой системе, полученная сумма будет минимальной. \(n\) можно взять сколь угодно большим и добиться требуемой точности (любой).

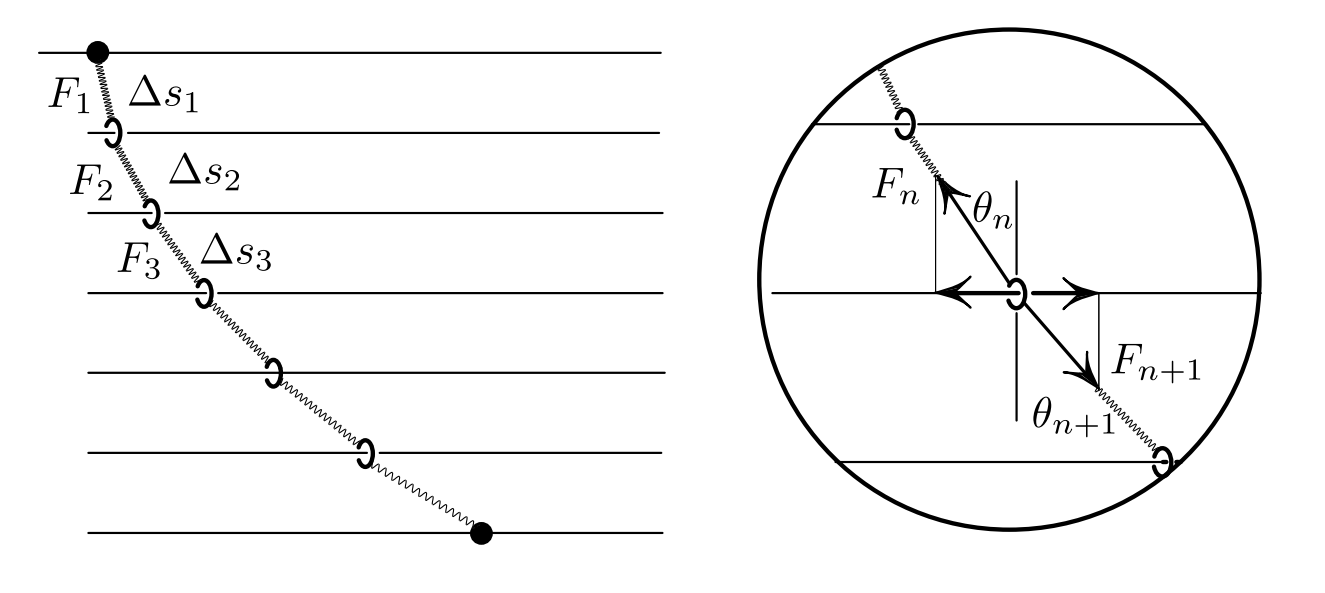
Рис. 3: Система пружин

Поскольку система в равновесии, горизонтальные проекции сил в каждой точке соединения скомпенсированы. То есть, \(F_k\sin\theta_k = const\), что и требовалось выяснить.

4.5. Брахистохрона

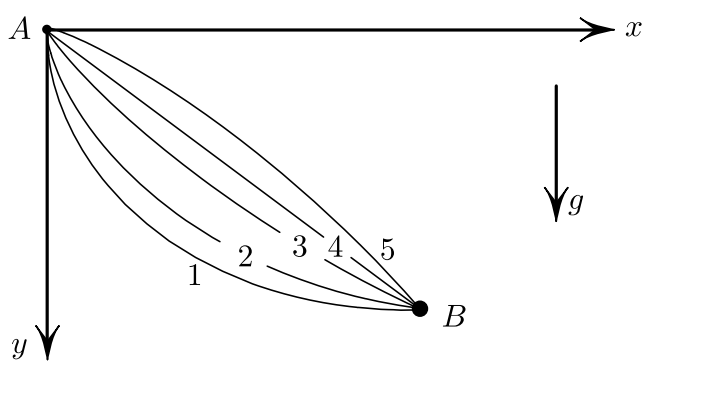
Рис. 4: Поиск брахистохроны

Брахистохрона — это кривая быстрейшего спуска от одной фиксированной точки к другой.

4.5.1. Теорема 4

Кривая быстрейшего спуска — циклоида.

Доказательство

Время движения материальной точки по кривой выражается интегралом:

\[ T = k\int_{AB}\frac{ds}{\sqrt{y}}=\int_{AB}\frac{ds}{v}, \;\;k=\frac{1}{\sqrt{2g}}, \]

где \(v=v(y)\) - скорость, ее определяет закон сохранения энергии:

\[ \frac{v^2}{2}-mgy=const. \]

Для ситуации справедливо утверждение \( \frac{F(y)}{\sqrt{1 + y'^2}} = F(y)\sin\theta = const \). Тогда:

\[ \frac{\sin\theta}{\sqrt{y}}=const. \]

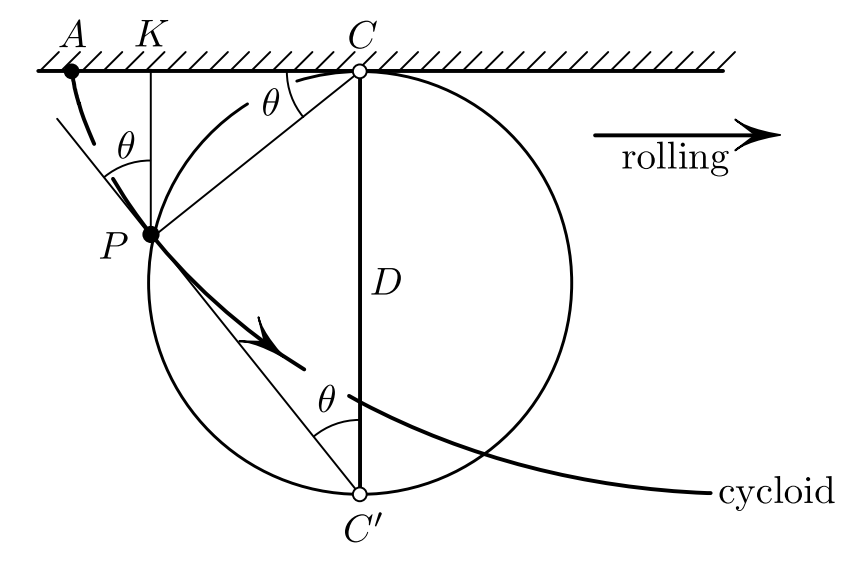
Рис. 5: Иллюстрация к доказательству. Циклоида.

Указанное выше соотношение справедливо для циклоиды. В самом деле, выразим \(PC\): \(y/\sin\theta\), \(D\sin\theta\), откуда следует:

\[ \frac{\sin^2\theta}{y}=D^{-1}. \]

На самом деле сейчас мы доказали лишь то, что циклоида является критической функцией, минимизация требует дополнительного исследования.

4.6. Историческое доказательство

Задача была опубликована Бернулли несколько веков назад (но не впервые им сформулирована), рассмотрим его решение. Он воспользовался оптической аналогией: луч света движется в среде со скоростью \(c = \sqrt{2gy}\), то есть со скоростью материальной точки. Тогда уже было известно, что свет выбирает кратчайшую дорогу, а также оптические законы, в частности, закон Снелла:

\[ \frac{\sin\theta_n}{c_n}=\frac{\sin\theta_{n+1}}{c_{n+1}}. \]

Подставляем одно в другое и получаем нужный результат. Лаконично и приятно.

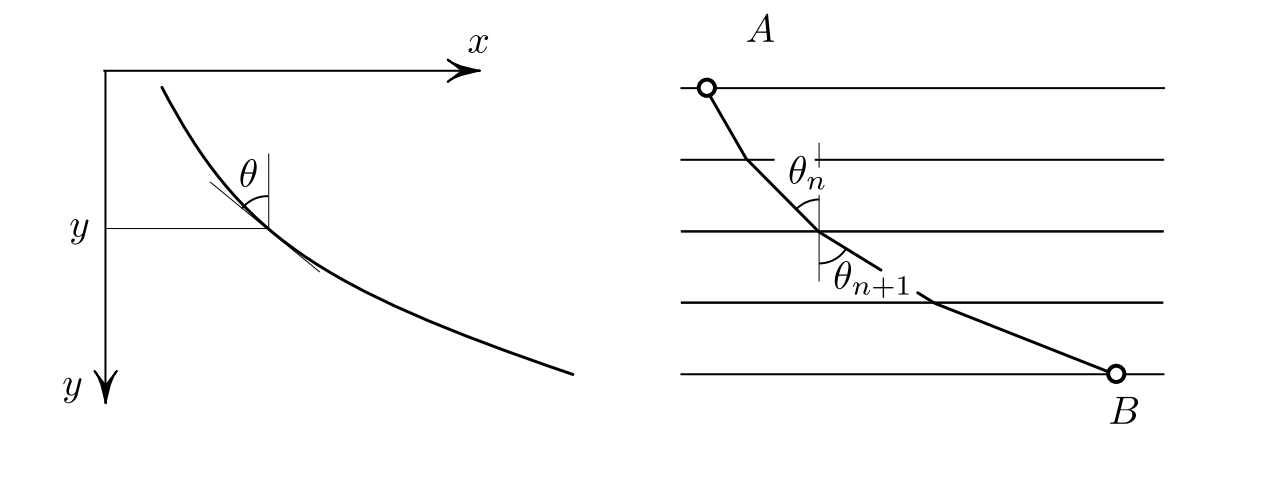
Рис. 6: Иллюстрация к доказательству Бернулли