1. Гравитационное линзирование

1.1. Введение

Почему интересно исследовать гравитационное линзирование? Это явление позволяет находить интересные объекты внутри нашей галактики: блуждающие черные дыры, экзопланеты. Во внегалактической астрономии гравитационные линзы позволяют ответить на вопросы, связанные со структурой массивных объектов: галактик, галактических кластеров (скоплений). Кроме того, гравитационное линзирование имеет и историческое значение: отклонение изображения звёзд Солнцем стало одним из первых надёжных свидетельств в пользу общей теории относительности.

В работе рассматриваются некоторые вопросы, связанные с гравитационным микролинзированием. В частности, выводятся основные соотношения, такие как радиус Эйнштейна, характеристики изобраажения, получено аналитическое представление о кривой блеска события микролинзирования. Кроме того рассматривается вопрос о интерференции на гравитационной линзе. Также проведено численное моделирование явления: получена кривая блеска, динамика изображения точечного и протяженного источника.

1.2. Уравнение линзы

Рассмотрим точечную массу \(L\) и точечный источник \(S\), излучение которого искажается массой на пути к наблюдателю \(O\), см. Рис. 1.1.

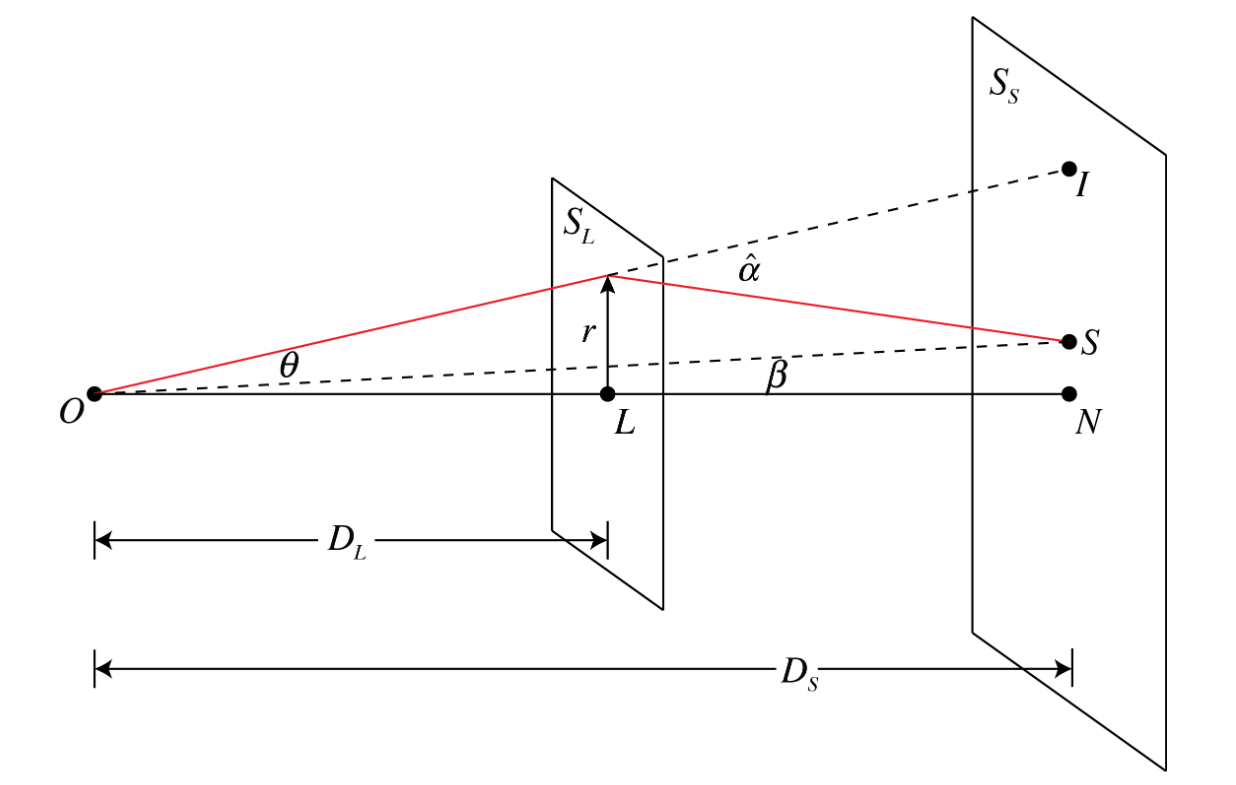
Рис. 1.1 Схема события микролинзирования в приближении малых углов. \(O\) — наблюдатель, \(L\) — точечная масса (линза), \(S\) — источник. Красная линия показывает путь преломленного луча.

Будем рассматривать ‘микролинзирование’ — аналог модели тонкой линзы, справедливы положения параксиального приближения. Так из чертежа следует соотношение:

(1.1)\[ \beta D_S=\theta D_S-\hat\alpha(D_S-D_L). \]

Здесь \(\theta\) — видимое угловое расстояние между линзой и источником, \(\beta\) — реальное. \(\hat\alpha\) — отклонение луча.

Для отклонения луча из соображений классической механики и из ОТО можно получить следующее соотношение (отличие классической теории от ОТО выражается в коэффициенте: \(2\) для первого, \(4\) для второго):

(1.2)\[ \hat\alpha = \frac{4Gm}{c^2r}=\frac{4Gm}{c^2D_L\theta}. \]

\(r\) — прицельный параметр, см. чертеж.

Подставляем (1.2) в (1.1):

(1.3)\[ \beta = \theta - \frac{4Gm}{c^2D_L\theta}\frac{D_S-D_L}{D_SD_L} = \theta - \alpha(\theta). \]

1.3. Кольцо Эйнштейна

Рассмотрим случай, когда источник находится в точности за линзой: \(\beta = 0\). Тогда:

(1.4)\[ \theta = \alpha(\theta) = \frac{4Gm}{c^2D_L\theta}\frac{D_S-D_L}{D_SD_L}. \]

Откуда следует:

(1.5)\[ \theta_E = \sqrt{\frac{4Gm}{c^2D_L}\frac{D_S-D_L}{D_SD_L}}. \]

Положим, что линза солнечной массы находится на расстоянии 4 пк от Земли, источник точно за ней на расстоянии 8 пк от Земли. Тогда \(\theta_E\approx1\)mas. Чтобы разрешить кольцо потребуется телескоп с диаметром зеркала \(D=1.22\lambda/2\theta_E\approx 60\)м. С Земли такое угловое разрешение получить не удастся, а в космос мы научились запускать зеркала на порядок меньшие (например, JWST имеет диаметр 6.5 м).

Однако для внегалактических объектов наблюдать кольца Эйнштейна вполне возможно, см. Рис. 1.2

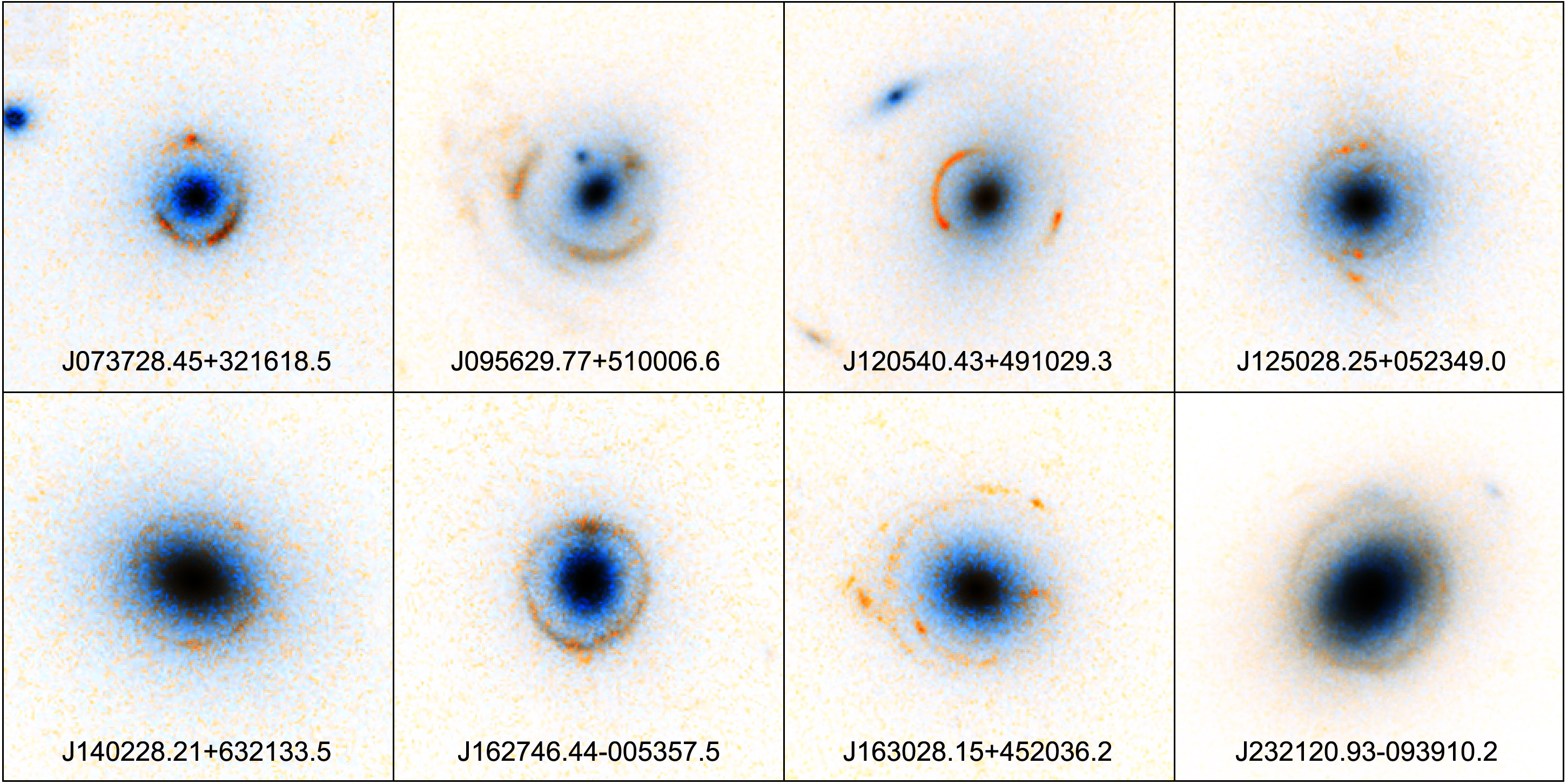
Рис. 1.2 Кольца Эйнштейна.

Для дальнейших рассуждений будет полезно вычислить радиусы Эйнштейна в проекциях на плоскость линзы и источника:

(1.6)\[ r_{EL} = \theta_ED_L;\;\;r_{ES} = \theta_ED_S. \]

1.4. Общая структура изображения

Фактически мы рассмотрели два случая: при \(\beta \approx 0\) мы видим кольцо, при \(\beta\gg\theta_E\) исходное изображение будет незначительно отклоняться и всё еще будет точкой. Интересно рассмотреть промежуточную ситуацию, когда \(\beta\approx\theta_E\).

Перепишем уравнение (1.3) следующим образом:

(1.7)\[ \theta^2-\beta\theta-\theta_E^2 = 0. \]

Решение уравнения относительно \(\theta\) имеет вид:

(1.8)\[ \theta_\pm=\frac{\beta}{2}\pm\theta_E\sqrt{1+\frac{\beta^2}{4\theta_E^2}}. \]

При \(\beta\sim\theta_E\) имеем два решения, причем одно положительное, а другое отрицательное. Причем \(\theta_+>\theta_E\), а \(\theta_-<\theta_E\), см. Рис. 1.3

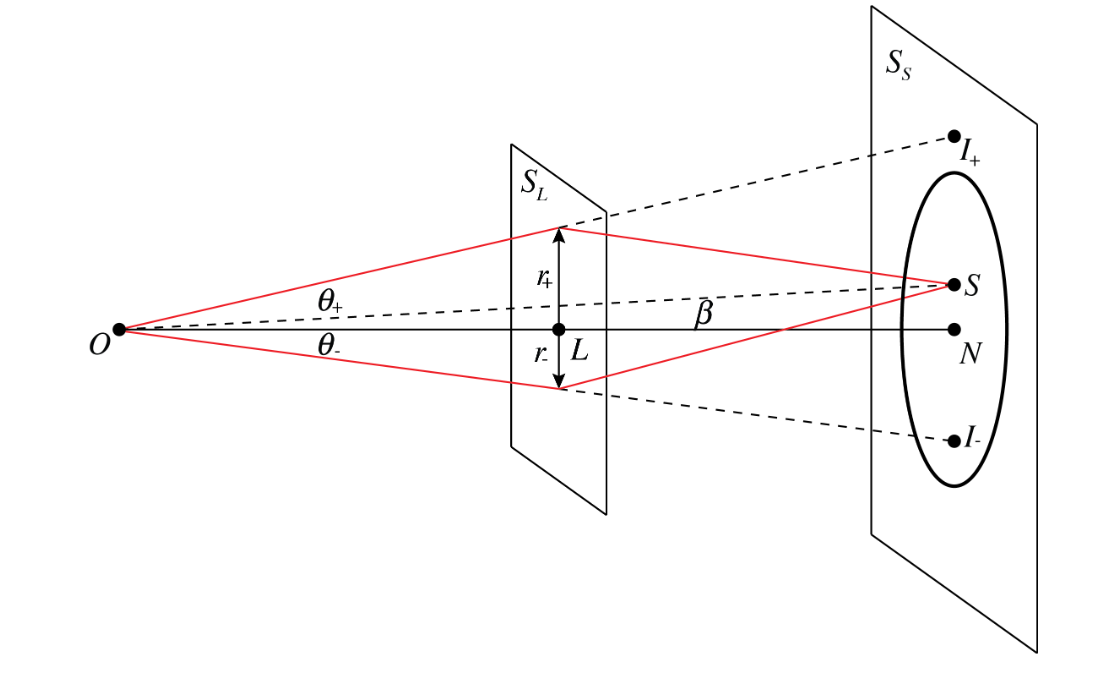
Рис. 1.3 Общая структура изображения при микролинзировании. Кольцо на плоскости источника — проекция кольца Эйнштейна.

Отметим, часто бывает так, что \(r_-\) мало и второе изобржение попадает в тень линзы, тогда наблюдатель не сможет его наблюдать.

Угловое расстояние между изображениями источника:

(1.9)\[ \Delta\theta = \theta_+-\theta_-=2\theta_E\sqrt{1+\frac{\beta^2}{4\theta^2_E}}. \]

Из этого соотношения следует, что если \(\beta<\theta_E\), то оба изображения попадут на кольцо Эйнштейна и, скорее всего, сольются.

1.5. Усиление сигнала

В ходе событий микролинзирования отмечается рост яркости источника.

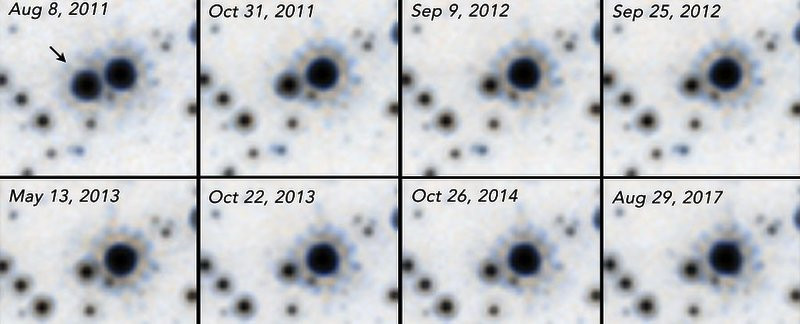
Рис. 1.4 Событие микролинзирования, вызванное прохождением черной дыры. Заметен значительный рост яркости слабого объекта.

Пропробуем ответить на вопрос, почему это происходит. Поток, приходящий от объекта можно расписать так: \(F=B_\Omega\Omega\), где \(B_\Omega\) — поверхностная яркость, \(\Omega\) — телесный угол, под которым наблюдается объект.

Как известно, поверхностная яркость объектов в обычных условиях не меняется при изменении расстояния, можно предположить, что здесь это также сработает.

Тогда яркость объекта будет зависеть от его углового размера (площади).

Введём коэффициент усиления:

(1.10)\[ A=\frac{d\Omega}{d\Omega_0}. \]

Смысл происходящего будет более понятен, если посмотреть на Рис. 1.5

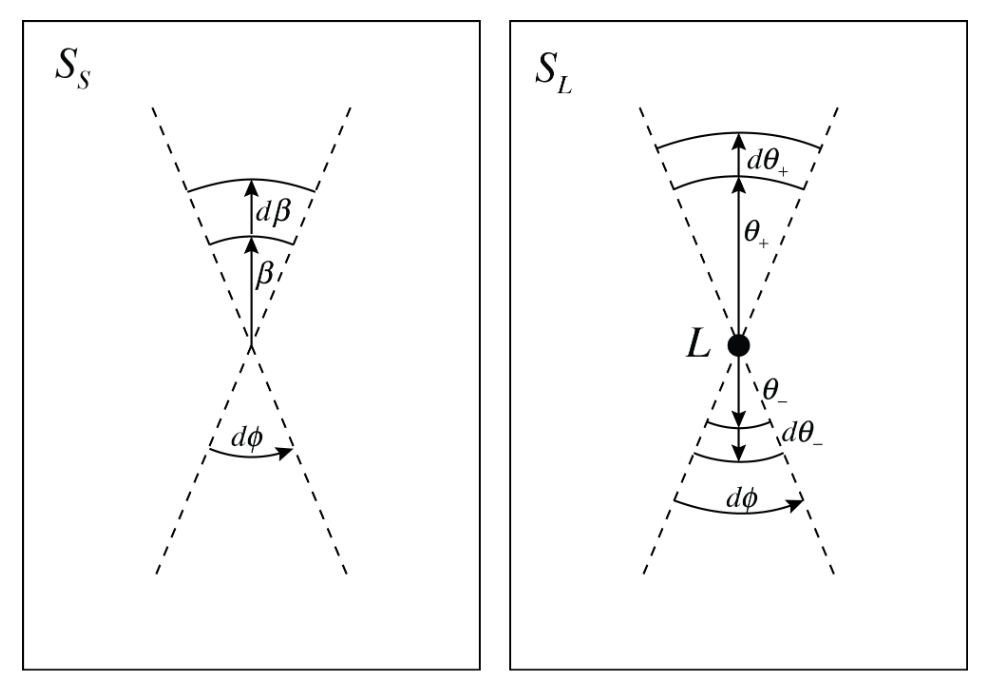
Рис. 1.5 Преобразование элемента площади источника гравитационной линзой. Введена полярная система координат на плоскости источника и линзы. Видно, что одному элементу площади источника соответсвует два элемента площади изображения в плоскости линзы.

Из рисунка следует:

(1.11)\[ A_\pm = \frac{\theta_\pm d\theta_\pm}{\beta d\beta}. \]

Из (1.8) получается:

(1.12)\[ A_\pm = \frac{1}{2}\pm\frac{\beta^2+2\theta_E^2}{2\beta\sqrt{\beta^2+4\theta_E^2}}. \]

Суммарное усиление:

(1.13)\[ A=|A_+|+|A_-|=\frac{\beta^2+2\theta^2_E}{\beta\sqrt{\beta^2+4\theta^2_E}}. \]

У полученного выражения есть один недостаток: при \(\beta\to0, A\to\infty\), что, конечно, не соответствует действительности. Однако при \(\beta\to\infty, A\to 1\), что справедливо.

1.6. Моделирование события микролинзирования

Чтобы убедиться в верности рассуждений необходимо провести численное моделирование и сравнить результаты с экспериментальными данными. Можно построить как само изображение точечного источника, искаженное линзой, так и кривую блеска явления.

Первым делом введём безразмерные величины, удобные для моделирования:

(1.14)\[ u = \frac{\beta}{\theta_E};\;\;y=\frac{\theta}{\theta_E}. \]

В новых переменных примем \(\theta_E=1\).

Положение изображения, соотношение (1.8), принимает вид:

(1.15)\[ y_\pm=\frac{u}{2}\pm\sqrt{1+\frac{u^2}{4}}. \]

Усиление, выражение (1.13), теперь выглядит так:

(1.16)\[ A=\frac{u^2+2}{u\sqrt{u^2+4}}. \]

В рамках нашей модели будем считать, что источник неподвижен, линза равномерно движется горизонтально в своей плоскости, перпендикулярной лучу зрения. Модель иллюстрирует Рис. 1.6

Рис. 1.6 Модель события микролинзирования: линза равномерно движется перед источником.

Из рисунка очевидна зависимость \(u(t)\) расстояния от источника до линзы:

(1.17)\[ u(t) = \sqrt{u_0^2+\frac{v^2}{r_{EL}^2}(t-t_0)^2}. \]

Здесь \(u_0\) — минимальное расстояние, разделяющее источник и линзу, \(t_0\) — момент, в который \(u(t)=u_0\).

Чтобы запись была еще удобнее, введем \(t_E=v/r_{EL}\) — время прохождения радиуса Эйнштейна линзой. Тогда (1.17) примет вид:

(1.18)\[ u(t)=\sqrt{u_0^2+\left(\frac{t-t_0}{t_E}\right)^2}. \]

Начнем с моделирования кривой блеска, на Рис. 1.7 представлены результаты расчета.

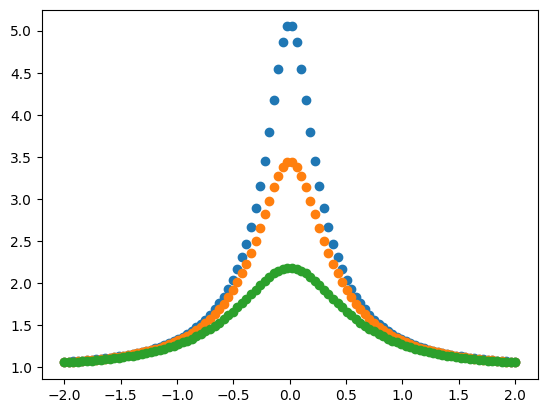
Рис. 1.7 Моделирование кривой блеска для события микролинзирования. По горизонтальной оси — нормированное время, по вертикальной — усиление сигнала. Три графика соответствуют значениям \(u_0: 0.2, 0.3, 0.5\).

В реальности кривые блеска таких событий очень похоже на полученные здесь, см. Рис. 1.8.

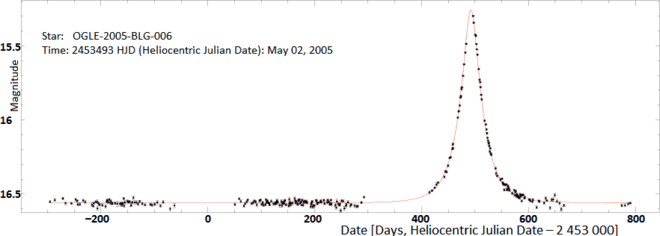
Рис. 1.8 Кривая блеска для события микролинзирования, полученная в ходе наблюдений.

На Рис. 1.9 представлены результаты моделирования изображения точечного источника в процессе микролинзирования.

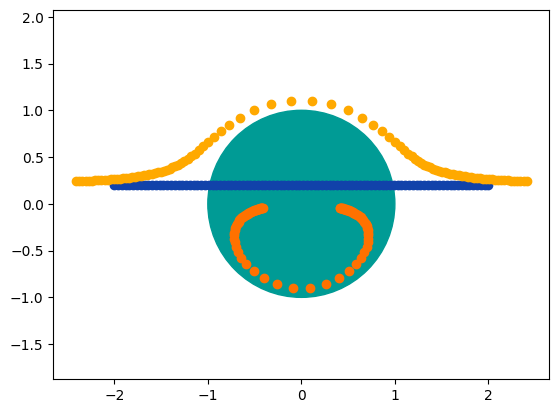
Рис. 1.9 Моделирование микролинзирования. Изображение источника, преломленного гравитационной линзой. Темные точки — траектория источника относительно линзы, темный круг — радиус Эйнштейна, две светлые группы точек — изображение источника, видимое наблюдателем.

Случай протяженного источника
В случае протяженного источника, преломляемого гравитационной линзой будут наблюдаться значительные искажения взаимного расположения его точек, это иллюстрируют Рис. 1.10 и Рис. 1.11.

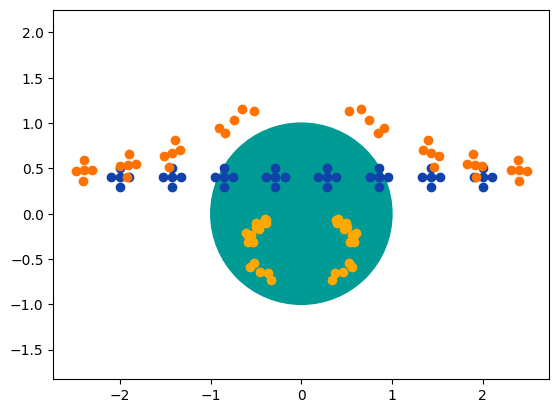
Рис. 1.10 Протяженный источник (представлен пятью точками) значительно искажается в процессе микролинзирования. Радиус источника \(0.1\), цветовые обозначения аналогичны предыдущему рисунку.

Рис. 1.11 Области, заметаемые протяженным источником в ходе гравитационного линзирования, радиус источника \(0.05\).

Интерференция на гравитационной линзе
Если посмотреть на Рис. 1.3, то можно увидеть сходство нашей схемы с опытом Юнга. Предлагаем рассчитать интерференцию в этом случае.
Разность хода между верхним и нижним маршрутом в нашем случае выражается не очень красиво, однако можно рассмотреть специальный случай: пусть \(D=D_L=D_S/2\), тогда разность хода примет вид:

(1.19)\[ \Delta = D\left(\frac{\theta_+^2}{2}+\frac{(\theta_+-2\beta)^2}{2}-\frac{\theta_-^2}{2}-\frac{(-\theta_-+2\beta)^2}{2}\right). \]

В этом выражении учтена малость некоторых членов, что позволило значительно его упростить.
Суммарное излучение в точке наблюдения складывается из двух, пришедших с разных направлений:

(1.20)\[ I=I_++I_-+2\sqrt{I_+I_-}\cos(2\pi \Delta/\lambda). \]

Очевидно, \(I\) немедленно ассоциируется с \(A\), обе величины обладают одинаковыми свойствами, необходимыми для построения интерференционной картины. На рис. 12 представлен пример такой картины.

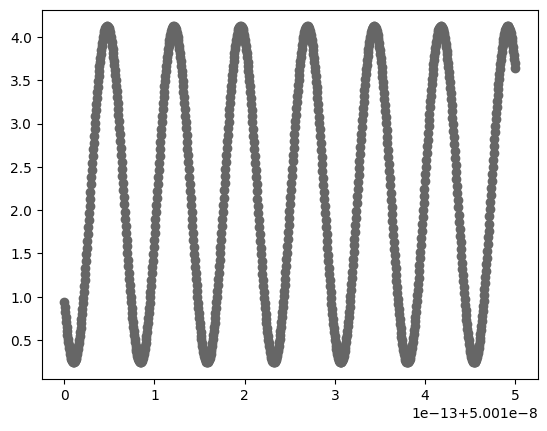
Рис. 1.12 Расчет интерференционной картины. \(\lambda = 10\) км, источник удалён на \(8\) пк, линза — на \(4\) пк. \(\theta_E = 10^{-7}\) рад. По горизонтальной оси отсчитывается \(\beta\), измеряемая в радианах, по вертикальной — суммарное усиление \(A\), см. соотношение (1.20).

Как видно, уже при \(\lambda = 10\) км наблюдаются очень частые осцилляции, что ограничивает возможность наблюдения явления. Однако, если мы говорим о линзировании на внегалактических объектах, допустимые дины волн могут спуститься до порядка \(1\) м (в силу космологических поправок), что в принципе может наблюдаться (см. например Gravitational Lens Interference, Peterson J. W., Toby Falk, PU, 1991.).