3. Математический анализ

3.1. Функции

3.1.1. Некоторые примеры функций

Пусть \(X\), \(Y\) — множества. Функция \(f\) определена на множестве \(X\) со значениями в \(Y\), если в силу правила \(f\) любому \(x\) из \(X\) соответствует единственный (это слово — единственное отличие функции от более общего понятия отображения) \(y\) из \(Y\). В таком случае также говорят, что \(X\) — область определения функции \(f\), а \(Y\) — область её значений. Это можно записать так:

\[ f:X\to Y. \]

Рассмотрим отображение следующего вида: \(G:\mathbb R^2\to\mathbb R^2\), причем области определения \(G\) будут принадлежать элементы \((x, t)\), а области значений — \((x', t')\). Такое отображение можно задать системой:

\[\begin{split} \begin{cases} x' = x+vt\\ t' = t.\\ \end{cases} \end{split}\]

Такое отображение в физике называется преобразованием Галлилея и необходимо для описания движения в нерелятивистском случае. По сути, это преобразование плоскости пространства-времени. Такое преобразование можно обобщить до преобразования 4-пространства, если добавить два дополнительных пространственных измерения.

Ещё один похожий пример, но тут отображение \(L:\mathbb R^2\to\mathbb R^2\) устроено чуть сложнее:

\[\begin{split} \begin{cases} x' = \frac{x-vt}{\sqrt{1-v^2/c^2}}\\ t' = \frac{t-vx/c^2}{\sqrt{1-v^2/c^2}}.\\ \end{cases} \end{split}\]

В физике такое отображение называют преобразованием Лоренца. \(v, c\) — фиксированные действительные числа (параметры).

Рассмотрим механическую систему из \(n\) частиц. Выражение для плоной механической энергии имеет вид: \(E = T+U\), где \(T\) имеет смысл кинетической энергии, а \(U\) — потенциальной. \(T\) и \(U\) зависят от набора координат и скоростей для каждой из частиц: \(\bar x\), \(\bar v\). В случае трехмерного пространства (геометрического), общее число переменных, описывающих состояние механической системы — \(6n\). Пространство, содержащее в себе числа, описывающие такие состояния называют фазовым пространством \(\Phi\subset\mathbb R^{6n}\). В таких терминах можно считать, что \(E\) — отображение, причем \(E:\Phi\to\mathbb R\), поскольку область значений \(E\) — обычные действительные числа.

3.1.2. Свойства отображений

Определение

Сюръекция — отображение \(f:X\to Y\) такое, что каждый элемент множества \(Y\) является образом хотя бы одного элемента из \(X\): \(\forall y\in Y\;\;\exists x\in X:\;\; y=f(x)\).

Иногда говорят: сюръекция — функция, принимающая все возможные значения.

Пример

\(f:\mathbb R\to\mathbb R,\;\;f(x)=x^2\) не является сюръекцией, поскольку \(y=-2\) не является образом никакого \(x\) (нет такого \(x\), что \(f(x)=-2\)).

Определение

Инъекция — отображение \(f:X\to Y\) такое, что \(\forall x_1,x_2\in X:\;\; f(x_1)=f(x_2)\Rightarrow x_1=x_2.\)

Иногда инъекцию называют одно-однозначным отображением.

Пример

\(f:\mathbb R_+\to\mathbb R,\;\; f(x)=x^2\) — инъекция, обратите внимание, что \(X\) — только положительные действительные числа.

Пример

\(f:\mathbb R\to\mathbb R,\;\; f(x)=x^2\) — не инъекция, поскольку \(f(-3)=f(3)=9\).

Определение

Биекция — отображение, явялющееся одновременно и сюръекцией и инъекцией.

Пример

\(f:\mathbb R\to\mathbb R,\;\; f(x)=x\), \(f:\mathbb R\to\mathbb R,\;\; f(x)=x^3\) — примеры биекций (это относится к любому моному нечетной степени).

Задача

Является ли сумма двух сюръекций сюръекцией?

3.2. Последовательности

3.2.1. Числовые последовательности

Определение

Последовательностью будем называть отображение \(x_n:\mathbb N\to X\).

То есть имеется в виду любой упорядоченный счётный набор элементов из \(X\).

Пример

Последовательность натуральных чисел тоже является последовательностью: \(1, 2, 3\cdots\)

Определение

Пределом последовательности \(a_n\) по Гейне называется число \(a_0\in X\) такое, что \(\forall U(a_0)\;\;\exists N\in\mathbb N:\;\; n\geq N\Rightarrow a_n\in U(a_0)\). Здесь под \(U(x)\) понимается окрестность числа \(x\): любое множество вида \((a,b)\), содержащее в себе \(x\).

Определение

Пределом последовательности \(a_n\) по Коши называется число \(a_0\in X\) такое, что \(\forall\varepsilon>0\;\;\exists N(\varepsilon)\in\mathbb N:\;\;n\geq N\Rightarrow |a_n-a_0|<\varepsilon\).

Можно показать, что два предложенных определения предела последовательности эквивалентны. По существу имеется в виду, что начиная с достаточно больших номеров числа последовательноси все ближе и ближе подходят к какому-то числу, причем само это число не обязано быть частью последовательности.

Обычно, когда говорят о пределе последовательности, вводится обозначение:

\[ \lim\limits_{n\to\infty}x_n=x_0. \]

Пределами последовательностей очень удобно оперировать: положим, что \(\lim\limits_{n\to\infty}x_n=A\), а \(\lim\limits_{n\to\infty}y_n=B\). Тогда справедливы следующие соотношения:

\[ \lim\limits_{n\to\infty}x_n+y_n=A+B, \]

\[ \lim\limits_{n\to\infty}x_n-y_n=A-B, \]

\[ \lim\limits_{n\to\infty}x_n\cdot y_n=A\cdot B, \]

\[ \lim\limits_{n\to\infty}\frac{x_n}{y_n}=\frac{A}{B}. \]

Задача

Чему равен предел последовательности \(x_n=\frac{1}{n^2}\)?

Задача

Чему равен предел последовательности \(x_n=\frac{n-3}{n+7}\)? Покажите это, пользуясь определением предела.

Определение

Последовательность называют фундаментальной (последовательностью Коши), если \(\forall\varepsilon>0\;\;\exists N(\varepsilon)\in\mathbb N:\;\;\forall n,m\geq N(\varepsilon)\;\; |a_n-a_m|<\varepsilon\).

Задача

Если последовательности имеет предел, то она фундаментальна. Покажите это, пользуясь определением предела.

Задача

Любая ли фундаментальная последовательность имеет предел?

3.2.2. Последовательности множеств

До этого момента мы работали с множествами и несколько раз сталкивались с последовательностями множеств. По смыслу они устроены так же, как и числовые последовательности и можно также говорить о пределах таких последовательностей. Этот аппарат имеет важную роль в конструктивных сюжетах и доказательствах, особенно в областях, смежных с топологией. Кроме того такой аппарат имеет и прикладное значение для физиков, когда мы говорим, например, о погрешностях измерений.

Всюду в этом разделе мы будем говорить о множествах на \(\mathbb R\).

Определение

Промежутком на \(\mathbb R\) называют множество \(X\), удовлеворяющее условию: \(\forall x\forall y\forall z (x\in X\land z\in X\land(x<y<z))\Rightarrow y\in X\).

То есть, если какое-то число лежит между двумя элементами промежутка, то и это число тоже принадлежит промежутку. Стандартное обозначение для промежутка: \(\lfloor a,b\rceil\).

Определение

Отрезком на \(\mathbb R\) называют множество \(X =[a,b] = \{x\in\mathbb R|a\leq x\leq b\}\).

Определение

Интервалом на \(\mathbb R\) называют множество \(X =(a,b) = \{x\in\mathbb R|a< x< b\}\).

Как видно из определения, отрезок отличается от интервала тем, что содержит в себе точки \(a\) и \(b\). И отрезок, и интервал являются промежутками. Иногда таже говорят о полуинтервалах: \([a,b) = (a,b)\cup a\), \((a,b] = (a,b)\cup b\), это тоже промежутки.

Зададим теперь последовательность интервалов:

\[ M_n = \left(-\frac{1}{n}, \frac{1}{n}\right). \]

Вполне очевидно, что при любом натуральном \(n\) \(M_n\) содержит в себе \(0\). В то же время для любой точки \(\varepsilon>0\) найдётся \(n\), начиная с которого \(M_n\) не будут его содержать. Аналогично для \(\varepsilon<0\). Получается, что

\[ M_n\to [0,0]\;\;\text{при}\;\;n\to\infty. \]

Здесь через нотацию отрезка записан интервал нулевой длины, точка, это вполне соответствует данному ранее определению отрезка.

Несложно рассмотреть похожий случай:

\[ M_n' = \left(a+\frac{1}{n}, b-\frac{1}{n}\right). \]

Такая последовательность интервалов сойдётся к отрезку \([a,b]\). К тому же отрезку сойдётся и такая последовательность:

\[ M_n'' = \left(a-\frac{1}{n}, b+\frac{1}{n}\right). \]

Различие в том, что элементы \(M_n'\) целиком содержатся в \([a,b]\), в то время как элементы \(M_n''\) содержат в себе этот отрезок. Условно это можно назвать внутренним и внешним накрытием отрезка. Впрочем, можно предложить совсем забавный вариант последовательности, сходящейся к \([a,b]\):

\[ \mathcal M_n = \left(a+\frac{(-1)^n}{n}, b+\frac{-(-1)^n}{n}\right). \]

Задача

При каких \(n\) интервалы из \(\mathcal M_n\) содержат в себе \([a,b]\)?

3.2.3. Неравенство Бернулли

Теорема

Пусть \(x\geq -1\) и \(n\in\mathbb N\). Тогда \((1+x)^n\geq 1+nx\).

\(\vartriangleright\) При \(n=1\) утверждение очевидно выпоняется. Положим теперь, что утверждение верно для \(n-1\):

\[ (1+x)^{n-1}\geq 1+(n-1)x. \]

Домножим обе части на \(1+x\):

\[ (1+x)^n\geq (1+(n-1)x)(1+x) = 1+nx+(n-1)x^2. \]

Очевидно, что

\[ 1+nx+(n-1)x^2\geq 1+nx. \]

То есть:

\[ (1+x)^n\geq 1+nx \]

Это значит, что утверждение теоремы доказано из принципа математической индукции.

\(\square\)

Теорема выше носит название неравенства Бернулли и весьма востребована, нам она поможет вычислить некоторые интересные пределы.

Теорема

Последовательность \(\left(1+\frac{a^n}{n}\right)^n\) стремится к \(1\), если \(a_n\) стремится к нулю при \(n\to\infty\).

\(\vartriangleright\) Применим неравенство Бернулли:

\[ \left(1+\frac{a_n}{n}\right)^n\geq 1+a_n. \]

В частности, \(x=\frac{a_n}{n}\) в терминах предыдущей теоремы, при умножении на \(n\) в правой части остаётся только \(a_n\).

Заметим теперь, что:

\[ \left(1+\frac{a_n}{n}\right)\left(1-\frac{a_n}{n}\right)=1-\frac{a_n^2}{n^2}\leq 1. \]

Разделим теперь всё на \(\left(1-\frac{a_n}{n}\right)\) и возведем в степень \(n\):

\[ \left(1+\frac{a_n}{n}\right)^n\leq \left(1-\frac{a_n}{n}\right)^{-n}. \]

Очевидно, что:

\[ \left(1-\frac{a_n}{n}\right)^{-n}\leq (1-a_n)^{-1}. \]

Соберем теперь полученные неравенства в подходящий вид:

\[ 1+a_n\leq \left(1+\frac{a_n}{n}\right)^n \leq (1-a_n)^{-1}. \]

Самая левая и самая правая последовательности стремятся к \(1\). Значит, согласно теореме о двух милиционерах:

\[ \left(1+\frac{a_n}{n}\right)^n\to 1\;\;\text{при}\;\; n\to\infty. \]

\(\square\)

Пример

Последнее утверждение можно использовать, чтобы показать одно из важных свойств экспоненты. Напомним её определение (одно из):

\[ \exp(x) = \lim\limits_{n\to\infty}\left(1+\frac{x}{n}\right)^n. \]

Покажем, что \(\exp(x)\exp(-x)=1\). Согласно определению, левую часть можно записать так:

\[ \left(1+\frac{x}{n}\right)^n\left(1-\frac{x}{n}\right)^n=\left(1-\frac{x^2}{n^2}\right)^n. \]

В терминах предыдущей теоремы, \(a_n = -\frac{x^2}{n}\). На \(a_n\) наложено требование: последовательность должна стремиться к нулю при \(n\to\infty\). Это выполняется, поскольку \(x\) в нашем случае — фиксированный параметр. Это сразу же позволяет сказать, что предел такой последовательности — \(1\), а значит нужное свойство экспоненты выполнено.

3.3. Предел функции

Предел функции устроен так же как и предел последовательности. Далее будем говорить о функциях вида: \(f:\mathbb R\to\mathbb R\). Прежде всего дадим формальное определение предела функции.

Определение

\(A\in\mathbb R\) — предел функции \(f\) в точке \(x_0\), если \(\forall x_n\to x_0\) при \(n\to\infty \;(n\in\mathbb N, x_0\notin x_n)\;\; f(x_n)\to A\) при \(n\to\infty\).

Это определение предела функции по Гейне. Понимать можно так: какую бы мы ни выбрали последовательность аргументов \(x_n\), последовательльность значений функции \(y_n=f(x_n)\) сойдется к \(A\). Эквивалентное определение предела по Коши:

Определение

\(\lim\limits_{x\to x_0}f(x)=A\Leftrightarrow \forall\varepsilon>0\;\exists\delta=\delta(\varepsilon)>0:\;\; \forall x:\; (0<|x-x_0|<\delta)\Rightarrow(|f(x)-A|<\varepsilon)\).

Пример

Рассмотрим функцию \(f=\frac{1}{x^2}\). При \(x\to 0\) \(f\to\infty\). Это приводит нас к понятию бесконечности: рассмотрим последовательность \(x_n\), если \(\forall\varepsilon>0\;\;\exists N: \forall n>N\; x_n>\varepsilon\), то \(x_n\to\infty\). Именно это и происходит в случае \(f=\frac{1}{x^2}\): какое бы мы ни выбрали конечное число, всегда найдется бесконечно много элементов последовательности \(1/x_n^2\) больше этого числа (и любой другой последовательности аргументов, сходящейся к нулю).

Для этой же функции также верно, что \(f\to 0\) при \(x\to\infty\). Какое бы мы ни выбрали конечное \(x\), \(1/x^2\) будет больше нуля, однако для любого (сколь угодно малого) \(\varepsilon>0\) существует \(x(\varepsilon)\) такой, что для любого \(x>x(\varepsilon)\) будет верно: \(\varepsilon>1/x^2\).

Пример

Рассмотрим функцию, определяемую так:

\[\begin{split} D(x)=\begin{cases} 1& x\in\mathbb Q, \\ 0 & x\in\mathbb R\backslash\mathbb Q. \end{cases} \end{split}\]

Это функция Дирихле. Её замечательное свойство состоит в том, что она не имеет предела: в любой окрестности любого действительного аргумента \(x\) найдутся как \(y=1\), так и \(y=0\), то есть не удасться покрыть значения функции произвольно малой \(\varepsilon\)-окрестностью.

Задача

Покажите, что

\[ \frac{x^n}{a^x}\to 0\;\;(x\to\infty, \forall n\in\mathbb N, \forall a\in\mathbb R). \]

Указание: воспользуйтесь заменой \(q=\sqrt[n]{a}\).

Докажем следующее утверждение:

\[ \lim\limits_{x\to 0}\frac{\sin x}{x}=1. \]

\(\vartriangleright\) Основная задача — показать, что:

\[ \cos^2x<\frac{\sin x}{x}<1, \]

это позволит немедленно применить теорему о двух милиционерах и доказать желаемое.

Рассмотрим следующее построение:

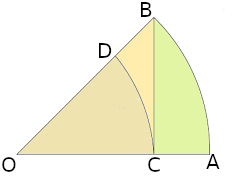
На единичной окружности отложим дугу \(AB\) длиной \(x\), \(O\) — центр окружности. Точка \(C\) — пересечение радиуса \(OA\) и высоты, опущенной на него. \(CD\) — дуга окружности с радиусом \(OC\).

Очевидно (из принципов построения тригонометрической окружности), что \(|OC| = \cos x\), длина дуги \(|CD|=x\cos x\), поскольку \(\cos x\) — радиус, а \(x\) — не только длина дуги единичной окружности, но и угол, отсекающий эту дугу. Тогда площадь сегмента окружности:

\[ S(OCD) = \frac{1}{2}|OC||CD|=\frac{1}{2}\cos x\cdot x\cos x=\frac{1}{2}x\cos^2x \]

Площадь этого сегмента меньше, чем площадь треугольника \(OAB\):

\[ S(OCD)<S(OAB) = \frac{1}{2}|OA||BC| = \frac{1}{2}\cdot 1\cdot\sin x = \frac{\sin x}{2}. \]

Площадь треугольника \(OAB\) в свою очередь меньше, чем площадь сегмента \(OAB\):

\[ S(OAB)<\frac{1}{2}|OA||AB|=\frac{1}{2}\cdot 1\cdot x = \frac{x}{2}. \]

Выпишем полученные неравенства вместе (множитель \(1/2\) общий, его можно отбросить, также разделим все части на \(x\)):

\[ \cos^2x<\frac{\sin x}{x}<1. \]

Может возникнуть вопрос, где это неравенство выполняется, а где нет, есть ли какие-то ограничения. В частности, из последнего выражения следует что (для обоснования также требуется вспомнить о нечетности \(x\) и \(\sin x\)):

\[ |\sin x|<|x| \]

при \(|x|<\pi/2\) (кроме нуля). Вспомним также, что \(|sin x|<1\) по определению. Это значит, что при \(|x|\geq\pi/2>1\) всё точно хорошо: \(|\sin x|<|x|\). Лишь в нуле \(\sin x = x = 0\). Из этого рассуждения следует, что

\[ \lim\limits_{x\to 0}\sin x = 0, \]

поскольку \(0\leq|sin x|\leq |x|\) везде. В качестве заключительного шага вспомним об основном тригонометрическом тождестве:

\[ \sin^2x+\cos^2x = 1\Rightarrow 1-\sin^2x\leq\frac{\sin x}{x}\leq 1. \]

Отсюда по теореме о двух милиционерах следует, что

\[ \lim\limits_{x\to 0}\frac{\sin x}{x}=1. \]

\(\square\)

3.4. Непрерывность

В физике мы почти всегда работаем с хорошими функциями. Одним из хороших свойств функции является непрерывность.

Определение

Функция \(f\) непрерывна в точке \(a\), если \(\forall U(f(a))\;\exists U(a): (f(U(a))\subset U(f(a))) \).

Это следует читать так: для любой окрестности точки \(f(a)\) найдется окрестность точки \(a\) такая, что все точки этой окрестности будут переведены функцией \(f\) в изначально выбранную окрестность точки \(f(a)\). Речь здесь идет, конечно, о \(f:\mathbb R\to\mathbb R\), хотя никто не мешает рассматривать непрерывность на отрезке. Определение непрерывности на языке окрестностей называется непрерывностью по Гейне. Эквивалентное ему определение непрерывности по Коши, а также промежуточный вариант:

Определение

\(f\) непрерывна \(\Leftrightarrow\) \(\forall\varepsilon>0\;\exists\delta>0:\;\forall x\in\mathbb R (|x-a|<\delta\Rightarrow |f(x)-f(a)|<\varepsilon)\).

Определение

\(f\) непрерывна \(\Leftrightarrow\) \(\forall\varepsilon>0\;\exists U(a):\;\forall x\in U(a) (|f(x)-f(a)|<\varepsilon)\).

Покажем, что \(f(x)=\sin x\) непрерывна на \(\mathbb R\).

\(\vartriangleright\) Выберем произвольно точку \(x_0\) на действительной прямой.

\[ |\sin x-\sin x_0| = \left|2\cos\frac{x+x_0}{2}\sin\frac{x-x_0}{2}\right|\leq 2\left|\sin\frac{x-x_0}{2}\right|\leq2\left|\frac{x-x_0}{2}\right|=|x-x_0|. \]

Полученное неравенство означает, что можно выбрать \(\delta(\varepsilon)=\varepsilon\) и непосредственно подставить его в определение непрерывности.

\(\square\)

Задача

Покажите, что \(f(x)=\cos x\) непрерывна на \(\mathbb R\).

С понятием непрерывности связано множество полезных утверждений и теорем. Одним из них является теорема Вейерштрасса (на самом деле множество теорем носят имя Вейерштрасса, здесь мы будем говорить о теореме Вейерштрасса о непрерывной функции на отрезке).

Теорема

Если функция \(f\) непрерывна на отрезке \([a,b]\) то она ограничена на нем и достигает своего минимума и максимума.

3.5. Дифференциируемость

3.5.1. Основные понятия

Рассмотрим линейную функцию следующего вида:

\[ \phi = A(x-a), \]

здесь \(A\) и \(a\) — некоторые действительные числа, причем под \(a\) подорозумевается некоторая точка на прямой (то есть \(x-a\) — направленное расстояние между точками \(x\) и \(a\)).

Определение

Дифференциалом функции \(f\) в точке \(a\) называют функцию \(\phi\) (обычно дифференциал обозначают символом \(df\)).

Однако нам подойдет не любая функция \(\phi\). Более того, для некоторых функций \(f\) и точек \(a\) такая функция может и вовсе не найтись.

Определение

Функция \(f\) называется дифференциируемой в точке \(a\), если существует \(\phi = A(x-a)\) такая, что \(F = f(x)-f(a)\) представима в виде:

\[ F = f(x)-f(a) = A(x-a)+o(x-a). \]

Здесь под \(o(x-a)\) подоразумевается любая функция, удовлетворяющая условию:

\[ \frac{o(x-a)}{x-a}\to 0\; \text{при}\; x\to a. \]

Иначе говоря, хочется, чтобы разность \(f-\phi\) была асимптотически мала: чем ближе мы к \(a\) (чем меньше \(|x-a|\)), тем меньше эта разница.

Вышесказанное можно сформулировать на языке пределов:

\[ \lim\limits_{x\to a}\frac{f(x)-f(a)}{x-a} = \lim\limits_{x\to a}\left(A+\frac{o(x-a)}{x-a}\right)=A. \]

Определение

Производной функции \(f\) в точке \(a\) называют предел:

\[ f'(a) = \lim\limits_{x\to a}\frac{f(x)-f(a)}{x-a}. \]

Вычислим производную функции \(f = x^2\) по определению.

\[ f'(a) = \lim\limits_{x\to a}\frac{f(x)-f(a)}{x-a} = \lim\limits_{x\to a}\frac{x^2-a^2}{x-a} = \lim\limits_{x\to a}x+a = 2a. \]

Тот же результат обычно получают из немного других соображений. Коль скоро мы говорим о свойствах функции \(f\) в точке, то можно говорить о локальности рассматриваемого явления. До этого момента мы полагали, что \(x\) — произвольная точка и выбирали последовательность таких точек, соходящуюся к \(a\). Выберем теперь \(x\) так, что это — произвольно мало отстоящая от \(a\) точка, то есть \(x-a = \varepsilon\) и будем решать задачу для произвально малого по модулю \(\varepsilon\).

Выразим \(x\) через \(a\) и \(\varepsilon\): \(x = a+\varepsilon\). Тогда справедливо:

\[ f'(a) = \lim\limits_{x\to a}\frac{x^2-a^2}{x-a} = \lim\limits_{\varepsilon\to 0}\frac{a^2+2a\varepsilon+\varepsilon^2-a^2}{\varepsilon} = \lim\limits_{\varepsilon\to 0} 2a+\varepsilon = 2a. \]

Это рассуждение также приводит нас к дифференциалу функции \(f=x^2\). Нужно представить \(F = f(x)-f(a)\) в виде \(F=A(x-a)+o(x-a)\). С учетом замены:

\[ F = f(x)-f(a) = f(a+\varepsilon)-f(a) = A(x-a)+o(x-a) = A\varepsilon+o(\varepsilon) = 2a\varepsilon+\varepsilon^2. \]

Таким образом нужный вид функции найден. В самом деле, \(\varepsilon^2 = o(\varepsilon)\), поскольку \(\varepsilon^2/\varepsilon = \varepsilon\), \(\lim\limits_{\varepsilon\to 0}\varepsilon = 0\).

\[ df = dx^2 = 2xdx. \]

\(dx\) в данном случае следует соотнести с \(\varepsilon\) непосредственно.

Задача

Вычислить производную и дифференциал для \(f = x-3x^2\) по определению.

3.5.2. Касательная

Важно отметить связь производной и касательной. При дифференциировании мы приближаем исходную функцию в точке некоторой линейной функцией \(\phi\), касательна тоже является линейной функцией (прямой). Угловой коэффициент такой прямой — \(A\), что ясно из определения \(\phi\). То есть вычисление производной функции в точке дает угловой коэффициент касательной. Почему указанная прямая соответствует определению касательной будет ясно из теоремы Лагранжа, с которой мы разберемся чуть ниже. Помимо углового коэффициента линейная функция характеризуется свободным членом (некоторой константой, численно равной значению линейной функции в нуле: \(f(0) = k\cdot0 + b\)). Чтобы найти его нужно приравнять значение искомой линейной функции в точке к значению исходной функции. Таким образом уравнение касательной к функции \(f\) в точке \(a\) имеет вид: \(y = kx+b\), где \(k = f'(a)\), \(f(a)=ka+b\).

Теорема

(Ролля) Если \(f\) непрерывна на \([a,b]\) и дифференциируема на \((a,b)\), а \(f(a)=f(b)\), то найдется \(x_0\in[a,b]\) такая, что \(f'(x_0)=0\).

\(\vartriangleright\) В случае \(f=const\) утверждение очевидно (производная константы всюду равна \(0\)). В иных случаях выполнены условия теоремы Вейерштрасса о непрерывной функции (упоминается в разделе о непрерывности), а значит функция достигнет своего максимального и минимального значения на отрезке \([a,b]\), а также ограничена на нем. Коль скоро функция не является всюду константой, значит есть точки, где \(f'\neq 0\). Но если есть точки с \(f'>0\), то должны быть и точки с \(f'<0\), поскольку если производная имеет постоянный знак на отрезке, то она будет монотонно расти (или убывать) и \(f(x)>f(a)\;\forall x\in(a,b]\) (\(f(x)<f(a)\;\forall x\in(a,b]\)), что противоречит условию \(f(a)=f(b)\). Тогда, если есть точки с различными знаками производной, то должна найтись хотя бы одна точка \(c\in[a,b]\), где \(f'(c) = 0\), а с разных сторон будут различные знаки производной.

\(\square\)

Теорема

(Лагранжа о среднем) Пусть функция \(f\) непрерывна и дифференциируема на отрезке \([a, b]\), тогда существует точка \(c\in [a,b]\) такая, что

\[ \frac{f(b)-f(a)}{b-a} = f'(c). \]

\(\vartriangleright\) Пусть

\[ A = \frac{f(b)-f(a)}{b-a}. \]

Тогда функция \(g(x) = f(x)-Ax\) удовлетворяет условиям теоремы Ролля. Непрерывность и дифференциируемость следуют из линейности выражения для \(g\) и выполнения этих свойств для \(f\). Также нужно рассмотреть разность:

\[ g(a)-g(b) = f(a)-f(b)-A(a-b) = 0. \]

То есть \(g(a)=g(b)\). Тогда по теореме Ролля найдется \(c\in [a,b]\) такое, что

\[ g'(c) = f'(c)-A = 0. \]

\(\square\)

Теорема Лагранжа может быть полезна в том числе в численном анализе функций: можно легко оценить производную функции в точке. Выбирается малый (относительно характерного масштаба задачи) отрезок, содержащий интересующую точку. Далее вычисляется число \(A\) (см. доказательство теоремы Лагранжа), являющееся оценкой производной: в точности это число равно производной в точке находящейся близко к изначальной.

3.6. Ряд Тейлора

Сформулируем такую задачу: попробуем представить произвольную функцию как сумму бесконечного числа очень простых функций, например, степенных:

\[ f(x) = a+bx+cx^2+dx^3\cdots. \]

Решим сперва частный случай задачи: рассмотрим только \(x=0\). Тогда в терминах такого разложения

\[ f(0) = a+b\cdot 0\cdots=a. \]

Возьмем производную функции:

\[ f'(x) = b+2cx+3dx^2\cdots, \]

тогда

\[ f'(0) = b, \]

аналогично:

\[ f''(0) = 2c, f'''(0) = 6d\cdots. \]

Это рассуждение приводит к выражениям для коэффициентов степенного разложения:

\[ a = f(0),\;b=f'(0),\;c=\frac{f''(0)}{2},\;d=\frac{f'''(0)}{6}\cdots. \]

Иначе это можно записать так:

\[ f(x) = \sum\limits_{n=0}^{\infty}\frac{f^{(n)}(0)}{n!}x^n. \]

Такое представление функции в окрестности нуля называют рядом Маклорена. Более общее выражение достигается заменой координат и позволяет разложить функцию в степенной ряд в окрестности произвольной точки \(a\):

\[ f(x) = \sum\limits_{n=0}^{\infty}\frac{f^{(n)}(a)}{n!}(x-a)^n. \]

Такое представление функции называют рядом (формулой) Тейлора. Оказыается, что практически все хорошие функции могут быть представлены рядом Тейлора. Класс таких функций называют аналитичными функциями, критерии соответствия этим функциям достаточно мягкие (их обсуждение выходит за рамки курса). Важно также отметить, что для всех функций разложение в ряд Тейлора единственно: если удалось найти какое-либо разложение, то другого не будет.

Важно отметить, что на практике редко используется весь ряд Тейлора (Маклорена). Обычно достаточно использовать сумму членов ряда до какого-нибудь небольшого \(n\): 1, 2, редко — 3. Оказывается, что оставшиеся члены ряда, не смотря на то, что их бесконечно много, в сумме малы. Если взяты члены ряда от \(0\) до \(n\), то все остальные члены ряда в сумме (остаточный член) будут удовлетворять условию для \(o(x^n)\), то есть остаточный член асимптотически мал.

Приведем некоторые ряды Маклорена:

\[ e^x = 1+\frac{x}{1}+\frac{x^2}{2!}+\frac{x^3}{3!}\cdots; \]

\[ \sin x = x-\frac{x^3}{3!}+\frac{x^5}{5!}\cdots; \]

\[ \cos x = 1-\frac{x^2}{2!}+\frac{x^4}{4!}\cdots. \]

Задача

Покажите, что для малых \(x\) справедливо приближение: \((1+x)^\alpha\sim 1+\alpha x\).

Задача

Найдите ряд Маклорена для \(f(x) = x^3-5x^2+0.12x\).

Задача

Объясните, почему \(\arcsin x = x+\frac{x^3}{3!}\cdots\). Воспользуйтесь рядом Маклорена для \(\sin x\).

Задача

Рядом Маклорена можно приближать функцию лишь в окрестности нуля. Насколько велика эта окрестность? Установите графически для \(e^x\) и \(\sin x\).