2. Сверхсветовое движение

2.1. Формулировка задачи

В вашем распоряжении серия снимков квазара 3C279 в радиодиапазоне.

1. Определите угловой размер ядра квазара и расстояние до него;

2. Какова наблюдаемая скорость вещества в джете?

3. Какова минимально возможная реальная скорость вещества в джете?

С учетом результатов СТО можно получить следующее выражение для видимой скорости объекта:

\[ v_{app} = \frac{v\sin\theta}{1-(v/c)\cos\theta}. \]

Здесь \(v_{app}\) — наблюдаемая скорость объекта, \(v\) — его реальная скорость, \(\theta\) — угол между лучом зрения и направлением реальной скорости, \(c\) — скорость света.

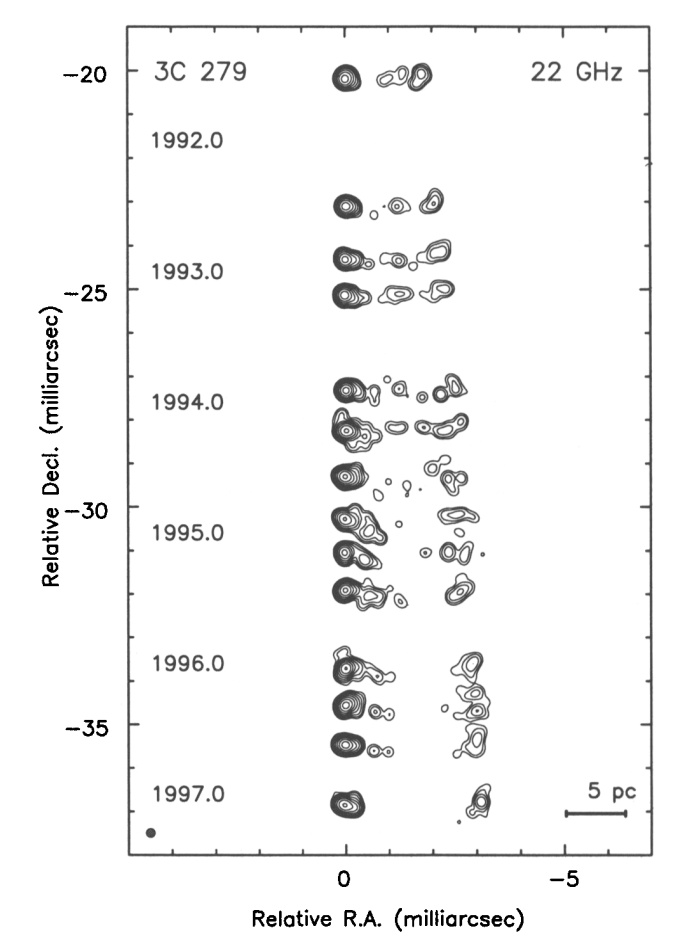
Рис. 2.1 Серия снимков квазара 3C279 в радиодиапазоне. Обратите внимание: для линейного и углового расстояния единичный отрезок указан отдельно!

2.2. Решение

2.2.1. Угловой размер

Угловой размер несложно определить, пользуясь шкалой. Обратите внимание, горизонтальная и вертикальная шкала имеют деления равного размера, что облегчает жизнь.

Ядром следует назвать область квазара с наибольшим градиентом яркости: там больше делений шкалы равных яркостей. Эта же часть имеет фиксированную координату по горизонтали.

Вторая, ‘подвижная часть’ — вещество джета. Его излучение на много порядков слабее излучения ядра, поэтому на самом деле шкала яркостей логарифмическая, что впрочем, к задаче не относится.

Размер ядра непосредственно составляет около \(1\) mas с точностью до особенностей структуры. Линейное расстояние также известно: около \(2.5\) пк (шкала расположена в нижнем правом углу графика, помечена: \(5\) pc).

Отсюда выражаем расстояние до объекта:

\[ D = \frac{l}{\gamma}, \]

где \(D\) — расстояние до объекта, \(l\) — линейный размер, а \(\gamma\) — угловой размер.

Отсюда \(D = 500\) Мпк или \(1.6\) Gly (гига световых лет).

2.2.2. Скорость вещества

Скорость вещества также несложно оценить: можно посчитать, на сколько увеличился разрыв между пятнами за все время наблюдения. Время отмечено слева, это годы. Такая прямая оценка скорости дает \(4.2\) c (имеется в виду скорость света), что кажется нереальным. Более точно эту величину можно вычислить, проведя прямую через пятно вещества и вычислив угол наклона в линейном законе движения.

Впрочем третий вопрос дает ответ на вопрос о физичности ответа: дело в конечности скорости света. Вывод соотношения на наблюдаемую скорость движения мы приводить не будем, однако заверяем, всё не так плохо :)

2.2.3. Реальная скорость вещества

Итак,

\[ v_{app} = \frac{v\sin\theta}{1-(v/c)\cos\theta}. \]

Немного модифицируем выражение: будем искать скорость сразу в единицах скорости света \(c\), тогда, согдасно нашему расчету:

\[ 4.2 = \frac{v\sin\theta}{1-v\cos\theta}. \]

Переносим множители:

\[ 4.2 - 4.2v\cos\theta = v\sin\theta, \]

\[ 4.2 = v(\sin\theta+4.2\cos\theta). \]

Получается, \(v\) будет минимальна, когда \(\sin\theta+4.2\cos\theta\) будет максимальным. Логично, что это выражение будет достигать максимума при большем вкладе от косинуса с множеителем \(4.2\) меньшем от синуса без множителя. В первом приближении можно сразу сказать, что \(\theta=0\), тогда \(v=1\), то есть скорость света. Однако это и так было понятно: не просто так пришлось обратиться к СТО)

Уточним результат, воспользовавшись формулами приближенного вычисления:

\[ \sin\theta\approx\theta,\;\;\;\cos\theta\approx 1-\frac{\theta^2}{2}, \]

\[ \sin\theta+4.2\cos\theta = \theta + 4.2 - 2.1\theta^2, \]

это квадратное уравнение, нужно найти его корни: пик параболы будет ровно между ними, поскольку каноническая парабола - четная функция. Он будет максимумом функции, поскольку коэффициент при \(\theta^2\) отрицательный (парабола ветвями вниз).

Если всё это посчитать — получаем оценку скорости \(v=0.973 c\), что хорошо сходится с результатами еще более точных расчетов.

2.2.4. Космологический комментарий

Читателям не составит труда открыть статью на википедии о квазаре 3C279 и обнаружить там чудовищное несоответствие: оказывается, расстояние до квазара составляет целых \(5\) Gly, что явно не соответствует полученному результату.

Чтобы устранить это недоразумение обратимся к космологии, в частности к закону Хаббла:

\[ cz = HD, \]

где \(c\) — скорость света, \(z\) — красное смещение, \(H\) — постоянная Хаббла, \(D\) — расстояние до объекта.

Чтобы достоверно посчитать \(z\) воспользуемся спектром квазара:

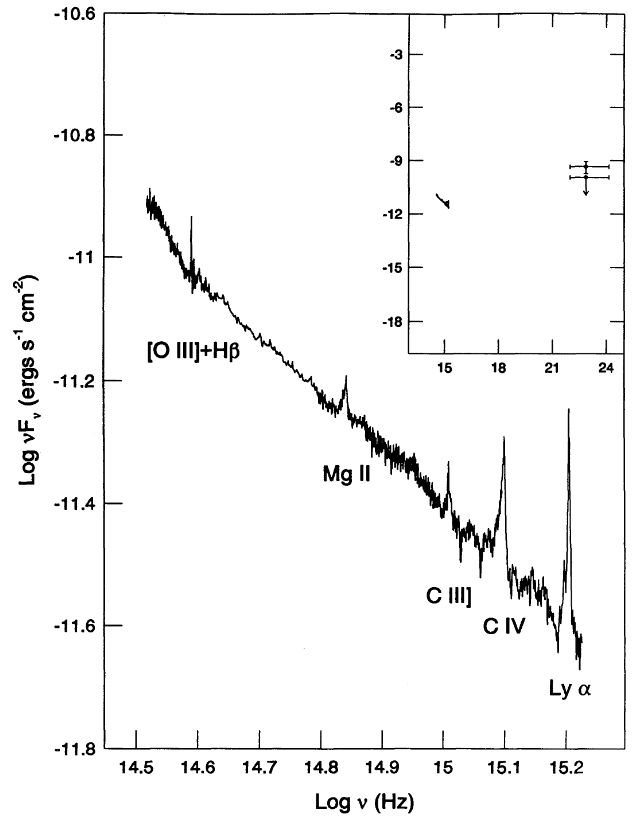
Рис. 2.2 Спектр квазара 3C279, указано соответствие эмиссионных линий и элементов. Обратите внимание: частота в логарифмическом масштабе!

Частоты линий \(H_\beta\) и \(Ly_\alpha\) обычно хорошо знакомы астрономам. Напомним определение красного смещения \(z\):

\[ z = \frac{\Delta\lambda}{\lambda}, \]

где \(\lambda\) — длина волны какой-нибудь линии, а \(\Delta\lambda\) — величина ее смещения на наблюдаемом спектре. Получаем \(z=0.535\), что уже соответствует википедии) Закон Хаббла теперь дает более хорошую оценку расстояния.

Такое несоответствие происходит из-за космологического искажения углового размера на больших расстояниях. В некотором приближении такое искажение выражается зависимостью:

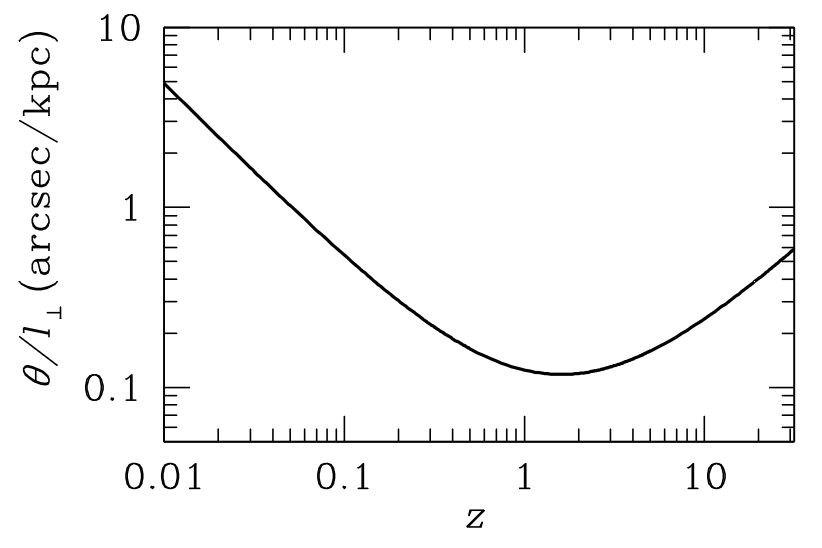
Рис. 2.3 Соотношение углового \(\theta\) и линейного \(l_\perp\) размера от величины красного смещения \(z\).

Определить коэффициент, сводящий результаты двух расчетов, читателю оставляем в качестве упражнения. Просто воспользуйтесь графиком)